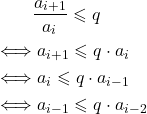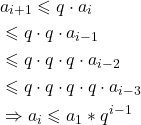Länge einer Kurve

Länge einer Kurve

Vektor-Analysis und Jordan-Kurven

Grundbegriffe der Vektoranalysis

Im Folgenden wird es um die Frage gehen, wie man die Länge einer Kurve bestimmen kann. Wir wissen aus den Grundlagen der Schulzeit, dass man die Länge eines Vektors mithilfe einer leichten Formel bestimmen kann. Diese haben wir zu Beginn als Euklidische Norm kennengelernt. Dieselbe Idee machen wir uns nun für Funktionen zunutze.

Parametrisierung von Kurven in $\mathbb{R}^n$

Zunächst müssen wir die zu vermessende Kurve jedoch in eine Form bringen, die es erlaubt die Länge zu bestimmen. Unser Beispiel ist dabei $\Psi (x)=x^2$ .
Es sei $[a,b] \in \mathbb{R}$ und $p:[a,b] \rightarrow \mathbb{R}^n$ eine stetige Funktion. Dann nennt man die Menge $K= \left\{ x \in \mathbb{R}^n \mid x = p(t), t \in [a,b] \right\}$ eine Parametrisierung.
Wie beschreibt man nun die Kurve, die diese Funktion $\Psi(x)$ in $\mathbb{R}^2$ abbildet?

Beispiel mit Kreis

Wenn wir uns die Umlaufende Strecke eines Einheitskreises vorstellen, dann wissen wir aus der Schulgeometrie, dass der Umfang des Kreises $2\pi$ beträgt. Wir können allerdings die Strecke des Umfangs auch wie folgt parametriesieren:

$\begin{align*}p_1 [0, 2\pi]: \ p_1 (t) = \binom{\cos (t) }{\sin (t)} \\\notag \\p_2 [0, 1]: \ p_2 (t) = \binom{\cos (2 \pi t) }{\sin ( 2 \pi t)}\end{align*}$

Wichtig ist zu erwähnen: Gemäß mathematischer Konvention laufen wir den Kreis damit entgegen des Uhrzeigersinns ab. Wollten wir mit dem Uhrzeigersinn gehen, dann müssen wir wie folgt umformen:

$\begin{align*}p_3 [0, 1]: \ p_3 (t) = \binom{- \sin (2 \pi t) }{\cos ( 2 \pi t)}\end{align*}$

Des Weiteren können wir den Kreis auch beliebig oft umlaufen. In diesem Beispiel 2-mal:

$\begin{align*}p_2 [0, 1]: \ p_2 (t) = \binom{\cos (4 \pi t) }{\sin ( 4 \pi t)}\end{align*}$

Ein Kreis hat natürlich mehr Radien als nur $r=1$ , weshalb wir den Radius mit in die Parametrisierung aufnehmen.

$\begin{align*}p_r [0, 1]: \ p_r (t) = \binom{r \cdot \cos (4 \pi t) }{r \cdot \sin ( 4 \pi t)}\end{align*}$

Elipse

Zitat Andrej: \textit{„Eine Ellipse ist auch nur ein Kreis, der einiges hinter sich hat“}. Diese Objekte lassen sich durch zwei Radien beschreiben, welche wir mit in die Parametrisierung aufnehmen.

$\begin{align*}E_1 [0, 2 \pi ]: \ e_1 (t) = \binom{a \cdot \cos (t) }{b \cdot \sin (t)}\end{align*}$

Äquivalenzklassen

Eine Kurze Bemerkung zu Äquivalenzklassen, da sich diese eignen, um das Vorgehen hier zu beschreiben. (genau def. im Skript)

Jordan-Kurven

Der Jordan’sche Kurvensatz

Wir stellen uns einen Kreis vor. Dabei beschreibt $\Omega_1$ das Gebiet außerhalb des Kreises, $\Omega_2$ das Gebiet innerhalb und $\Gamma$ die Kurve des Kreisrandes selbst. Wir halten fest:
\begin{itemize}
\item $\Omega_1 \cap \Omega_1 = \emptyset$
\item $\partial \Omega_1 = \partial \Omega_2 = \Gamma$
\item $\Omega_1 \cup \Omega_1 \cup \Gamma = \mathbb{R}^2$
\end{itemize}

Kurvenlängen

(Bild der Funktion und Kurve)

Sei $p: [a,b] \rightarrow \mathbb{R}^n$ , die Parametrisierung von $\Gamma$ . So ist die Zerlegung $Z$ wie folgt: $a=t_0 < t_1 < \cdots 0 \, \exists n_0 \in \mathbb{N}$ , sodass $|a_n - a_m | < \epsilon \, \forall n,m > n_0$ mit $n \rightarrow a_n \in \mathbb{R}$ . Des Weiteren gilt für den Grenzwert und die damit einhergehende Konvergenz einer Folge: $|a-a_m|<\epsilon \ \forall m>n_0, \ n \rightarrow \infty$ .

Kriterien für Konvergenz

$\begin{align*}\mathbf{S}_n = \sum_{i=1}^n a_i\end{align*}$

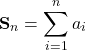
Reihen sind ja eigentlich zur spezielle Folgen, deren Eigenschaften bei Aufsummierung interessant sind. Wir betrachten noch einmal die harmonische Reihe.

$\begin{align*}\mathbf{S}_n = \sum_{i=1}^n \frac{1}{i}\end{align*}$

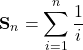
In Analysis-1 haben wir gelernt, dass ich Terme stets als Summen von $\frac{1}{8}$ zusammenfassen lassen und daher der Beleg geliefert wird, dass die Reihe divergiert. Grundsätzlich sagt man, dass eine Reihe konvergiert, genau dann wenn:

$\begin{align*}\quad \Longleftrightarrow |S_n - S_m|< \epsilon, \ \forall n,m > n_0 \\\quad \Longleftrightarrow |\sum_{i=1}^n a_i - \sum_{i=1}^m a_i |< \epsilon \\ \quad \Longleftrightarrow |\sum_{i=1}^n a_i | < \epsilon \end{align*}$

Dabei gilt, dass $n>m \geqslant n_0$ . Anders ausgedrückt, konvergiert eine Reihe, wenn die Summe der späten Glieder klein wird, also das $a_i \rightarrow 0$ für $i \rightarrow \infty$ .

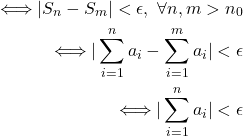
Wurzel-Kriterium

Betrachte speziell alle $a_i > 0$ . Es folgt die Konvergenz einer Reihe aus:

$\begin{align*}\sqrt[n]{a_n} \leqslant q < 1 \end{align*}$

Die Reihe ist damit durch $q$ und $q<1$ beschränkt. Wir beweisen dies, wie folgt:

$\begin{align*} \lvert \sum_{i=m+1}^n a_i \rvert \leqslant \sum_{i=m+1}^n q^i \\ \leqslant q^{m+1} \cdot \frac{(q^{n(m+1)}-1)}{q-1} \\ \leqslant q^{m+1} \left(\frac{1}{1-q}\right) \end{align*}$

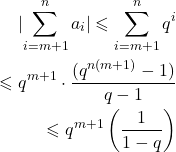
Majoranten-Kriterium

Aus dem Beweis des Wurzelkriteriums leiten wir das Majoranten-Kriterium ab. Dieses besagt im Grunde:

$\begin{align*} \lvert \sum_{i=m+1}^n a_i \rvert \leqslant q^{m+1} \left(\frac{1}{1-q}\right) \end{align*}$

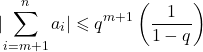
Quotienten-Kriterium

Zuletzt betrachten wir das Quotienten-Kriterium für die Abschätzung von Reihen. Konvergenz einer Reihe folgt aus diesem Zusammenhang:

$\begin{align*} \frac{a_{i+1}}{a_i} \leqslant q < 1 \end{align*}$

Der Beweis dazu vollzieht sich in zwei Schritten. Zunächst formen wir die obige Ungleichung geschickt um:

$\begin{align*} & \hspace{0.8cm} \frac{a_{i+1}}{a_i} \leqslant q \\ & \Longleftrightarrow a_{i+1} \leqslant q \cdot a_i \\ & \Longleftrightarrow a_i \leqslant q \cdot a_{i-1} \\ & \Longleftrightarrow a_{i-1} \leqslant q \cdot a_{i-2} \end{align*}$

Wir setzen nun von unten nach oben die Gleichungen für $a_{i-1}$ und für $a_i$ und erhalten so eine Kette von Ungleichungen, die anstelle von $a_i$ -Termen, eine gewisse Anzahl von $q$ enthält

$\begin{align*} & a_{i+1} \leqslant q \cdot a_i \\ & \leqslant q \cdot q \cdot a_{i-1} \\ & \leqslant q \cdot q \cdot q \cdot a_{i-2} \\ & \leqslant q \cdot q \cdot q \cdot q \cdot a_{i-3} \\ & \Rightarrow a_i \leqslant a_1 * q^{i-1} \end{align*}$

Maximilian R. Schlechtinger